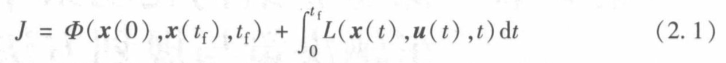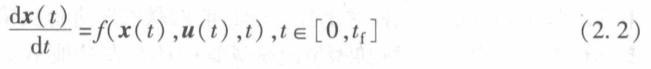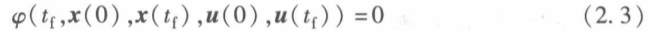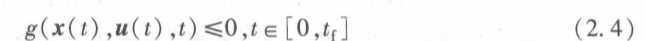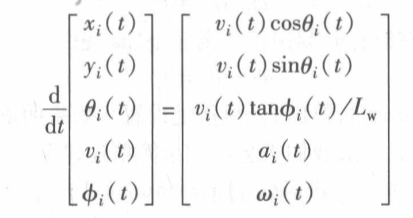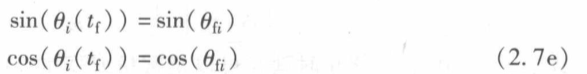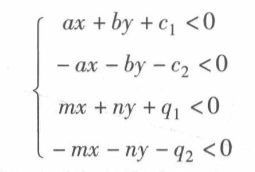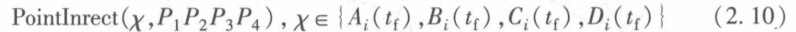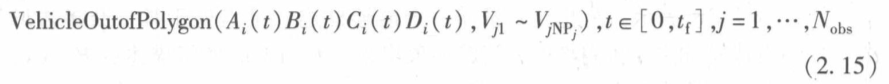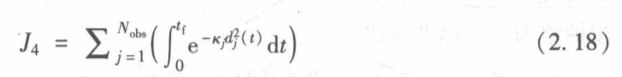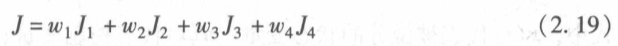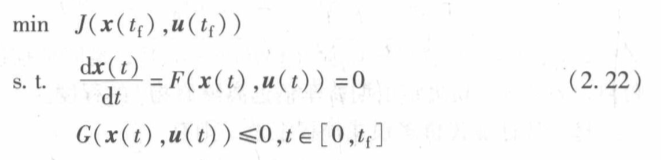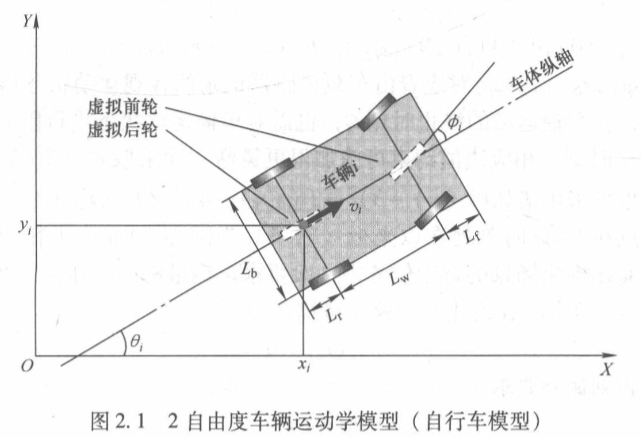
低速解构化场景中的单一车辆决策与规划

轨迹规划命题构建

车辆运动过程的最优控制问题属于连续[Bolza](博尔查问题_百度百科 (baidu.com))型问题，具有一下特征：
1)从状态方程类型来讲，它属于连续控制系统。
2)从性能指标类型来讲，它属于复合型性能指标。
3)从末端条件类型来讲，它属于末端受约束，且末端时刻可以不固定。
4)从系统函数类型来讲，它属于时变非线性系统。

Bolza 问题求解概述：

输入控制变量U(t),同时确定好终止时刻tf，使代价函数

沿着相应的状态轨线x(t)取得最小值。
约束包括：
系统动态方程约束（用于描述动力学/运动学约束）：

两点边值约束：

流行约束：

系统动态方程约束

两点边值约束

在充斥着障碍物的复杂场景中，我们一般无法提前预判车辆以何种“转圈”方式抵达终点，因此下面的描述更合理。

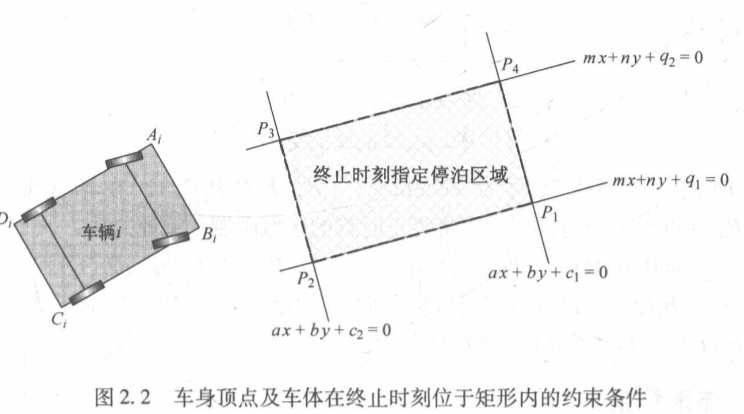
车库约束：

计算点在矩形内：

最终表达：

流行约束

流形约束是指作用于车辆运动过程中( 除系统动态方程之外)的约束条件,它们能够将状态/控制变量限制在解空间的某一流形上。

分别为，前轮转角、线加速度、行驶速度、前轮转角速度

障碍物描述：
常见的描述包括，散点集、网格图以及多边形，其中多边形描述障碍有利于构建解析形式的碰撞约束条件。散点集、网格图等其他格式的障碍物信息可经聚类、最小凸包生成等成熟算法转化为多边形障碍物。

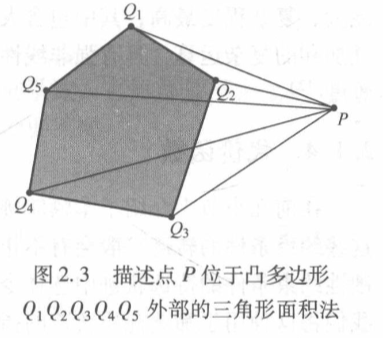
如何描述点与多边形的位置关系？
三角面积法。

最终形式：
代表车辆构成的矩形和各障碍之间的位置关系

代价函数

筛选优质轨迹的指标式。
时间约束：
轨迹平滑约束：

远离障碍约束：

最终加权：

最优控制完整形式

轨迹规划命题的数值求解

问题被抽象为：

式中，x(t)代表被微分的状态变量; u(t)代表控制变量; J为仅含有末值型指标式的代价函数; F代表常微分方程组中的代数函数部分; G包含了边值约束及流形约束; tf 代表动态过程的终止时刻，且tf可不固定。

最优控制问题求解方法
一般求解方法：间接法、动态规划法和直接法，直接法将原始命题式(2.22)中的连续变量部分或全部地离散化，通过求解，离散后形成的非线性规划(NonLinearProgramming, NLP)命题来直接得到式(2.22)的数值最优解。

全联立离散化

直接法可细分为：
部分离散 —贯序策略
完全离散—联立策略
全联立正交配置有限元法( Orthogonal Collocation Drect Transcription, OCDT)是以正交配置有限元的形式将最优控制问题中的所有状态/控制变量同时离散化、全部视作决策变量而联立求解的一种方法。

非线性规划

分为梯度优化和非梯度优化

梯度优化方法：
有效集法：序贯二次规划( Sequential Quadratic Programming, SQP )

障碍函数法：内点算法( Interior Point Method, IPM )
IPM的核心思想是将NLP问题中的不等式约束条件转化为惩罚项，在将其乘以相应障碍因子后补人目标函数中，从而将原NLP问题变为至多只包含等式约束新问题。至此求解原始NLP问题转变为求解一系列障碍因子取值不同的子问题。

X为决策变量，S为引入的松弛矢量