Optimal trajectory generation for dynamic street scenarios in a Frenét Frame

* Authors: [[Moritz Werling]], [[Julius Ziegler]], [[Sören Kammel]], [[Sebastian Thrun]]

初读印象

comment:: 自动驾驶车辆安全处理动态高速公路和内城场景涉及生成适应交通的轨迹的问题。为了满足全自主系统的实际需求，提出了一种可紧密集成到行为层的半反应式轨迹生成方法.该方法通过在街道的Frenet框架内的最优控制策略结合反应式防撞实现了长期目标，如速度保持、并道、跟随、停止。

文章骨架

%%创新点到底是什么?%%
novelty::我们的主要焦点不是在某个成本泛函的优化上。相反，我们在最优意义上用公式表示轨迹跟踪问题，以利用在随时间选择最佳可行轨迹时主张一致性的理论。有了这个，我们试图确保一旦找到最优解，它将被保留（贝尔曼的最优性原则）。对于汽车而言，这意味着它在每个计划步骤中遵循先前计算的轨迹的剩余部分，因此提供了时间一致性。

%%有什么意义？%%
significance::

%%使用了什么方法?%%
usage method::
横向运动
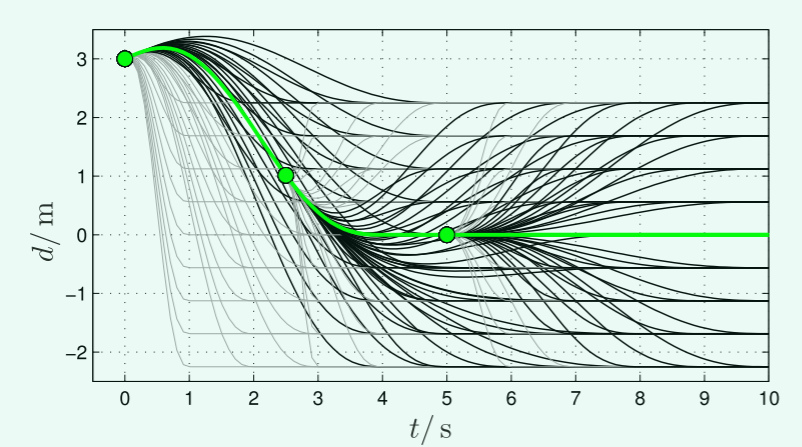
A.高速轨迹,代价函数
$$
C_d = k_jJ(d(t))+k_tT+k_dd_1^2
$$

B. 低速代价函数
$$
C_d = k_jJ_s(d(s))+k_tS+k_dd_1^2
$$

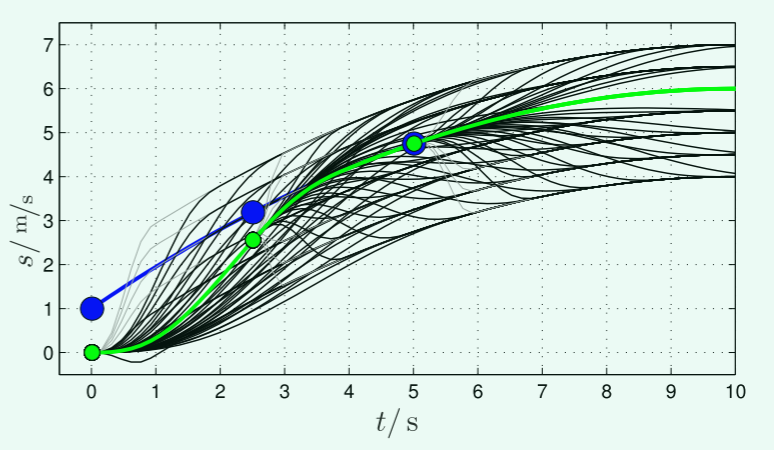
纵向运动
A：跟随、合并和停止
末状态：


代价函数：
$$
C_t = k_jJ_t+k_tT+k_s[s_1-s_d]^2
$$

跟车：通过积分预测目标未来轨迹
合并：计算两车中间的纵向位置

组合轨迹
代价函数：
$$
C_{lot} = k_{lat}C_{lat}+k_{lon}C_{lon}
$$

%%优点和缺点?%%
merits ::

demerits::

%%机构&作者%%
who::

%%未来展望%%
prospect::由于短优化层,然而,这种方法并不旨在缓解层有远见的决策行为。新的合适的启发式,比如constant-time-gap-law或保守合并检查,可以减少数量的关键情况下处理活性水平。更好的算法被集成到行为层和其他交通参与者可以更精确地预测,进一步我们可以提前与我们的测试车辆道路交通开放,这将显示接受的水平。

参考文献

[1] Werling M , Ziegler J , Kammel S , et al. Optimal Trajectory Generation for Dynamic Street Scenarios in a Frenet Frame[C]// Robotics and Automation (ICRA), 2010 IEEE International Conference on. IEEE, 2010.