运动规划古月

what is planning

• 本质
  $$
  argmin_{x}f(x)
  $$

• 搜索问题

• “好”其实就是一个目标函数：

  $$
  f(x)
  $$

  • f(x)的最优解

Motion planning 的三个跟踪领域

• Robotics Fileds:
  • 生成轨迹实现目标
  • RRT, A*, D* Lite
• Control Theory:
  • 动态系统理论实现目标状态
  • MPC，LQR
• AI: 生成状态和Action的一个映射
  • RL, Imitation Learning
    cited by motion planning by steve lavelle: https://planning.cs.uiuc.edu/part1.pdf

如何解决Motion planning问题？

• 找到简单的突破口

  • path finding problem
    • 不关心速度，不关心走
    • 周围固定

• 简而言之就是：路径选择问题

• A simple shortest path

  • 路径最短：BFS &DFS ; Dijkstra; A* search

• 无人车中的规划和A search 相差多远*

• 部分感知

• 动态障碍物

• 复杂环境：交通规则、碰瓷

基本planning 方法

• 经典基于环境模型的方法
• RRT
• Lattice
• 现代无人车planning 方法
• Darpa
• Lattice in Frenet Frame
• Spiral polynomial


• 质点模型
• 物体看成质点
• 点与点不碰撞
• 刚体问题
• BycicleModel
• XY Heading
• Collsion
• Planning 限制条件
• 避免碰撞
• 边界阈值
• 连续空间问题怎么解？
• 离散化
• 网格化

传统的机器人基础

• PRM

  • 连续空间离散化
    • 随机撒点
    • Obstacle 上的点删除
  • 连接可行点，形成可行空间
    • A*

• RRT（Incremental version of PRM）

  • 使用增量搜索的方式进行
  • 找附近可行点的最优点
    • F(x)最小， Cost最小
    • 走过程中并不能有阻碍使Cost 小
    • 走的过程中，还可能碰到障碍
    • 撒点距离不能太远
      • 一步一步移动

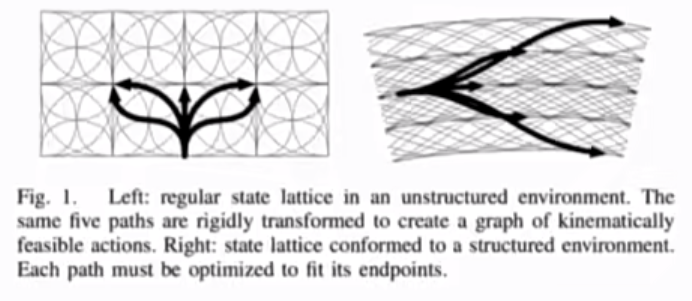
• Lattice 方法

  • 改进了RRT的折线问题
  • 给出Path 的平滑曲线
  • 网格化
    • 每个采样格用曲线连接
  • 指数级别搜索算法（NP-Hard）
  • 

• DP（动态规划）

  • 减少搜索空间
    • 复用已有结果
    • 
    • Lattice DP的平滑度够吗？
      • 曲率连续
      • 曲率导数不一定连续

• QP（二次规划）

  • 凸优化问题最优化求解

  • 公式表达

  $$
  minimize\frac{1}{2}X^TQX + c^TX \quad
  subject:Ex=d,F_x\leq{m}
  $$

  • 性质：在凸优化中的凸空间问题，用QP有最优解

• QP如何找到平滑曲线？
  $$
  min|\dot{f}|^2
  $$

  $$
  min|\ddot{f}|^2
  $$

  $$
  min|\dddot{f}|^2
  $$

  • 其它的平滑曲线方法还有贝塞尔曲线、样条插值方法

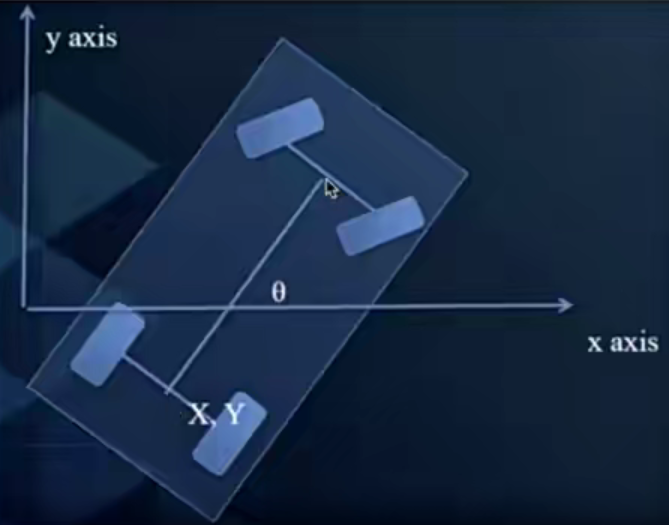
• 刚体模型

  • 

  • 前轮转向和Heading的关系

    • 车轮是沿切线方向行驶
    • 前后轮是同一旋转中心
    • 左右轮的结构相同

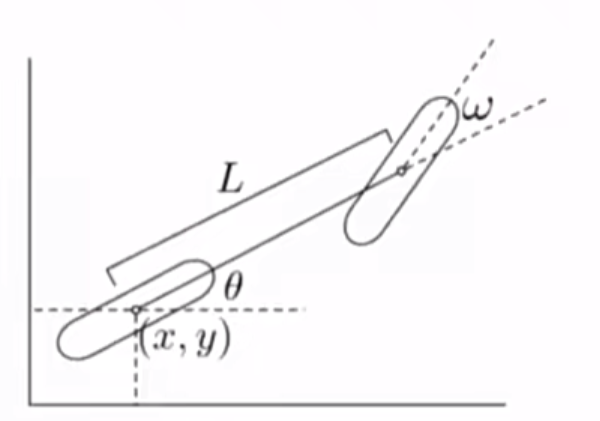
  • Bicycle Model

    • 

    • 曲率公式：

      • $$
        1/R=kappa=(tan(w)/L)
        $$

无人车Planning

• 定义

  • A点到B点，构建车辆运动轨迹，结合HDMap,Localization和Prediction
  • 输入
  • 输出：可行是轨迹，有一系列点组成
  • 两个层面：导航层面；运动轨迹层面

• Routing

  • 导航A点到B点的全局路径
  • 输入：地图（路网信息，交通状态）、当前位置、目的地
  • 输出：可行驶道路的连接线
  • 搜索：地图数据转换成图网络
    • 节点表示道路
    • 边表示道路连接

• A 经典算法*

  • $$
    F(n)=G(n)+H(n)
    $$

• Motion Planning

  • 
  • Planning 理解为高精度、低级别的一个search , trajectory Planning
  • 轨迹点：XY、Time、Velocity

• 轨迹约束条件

  • Collsion 碰撞
    • 躲避任何障碍物
  • Comfortable 舒适
    • 路径点必须相对平滑、速度也要平滑
  • 运动动力学约束
    • 高速转弯、掉头曲率
  • Illegal 合法
    • 交通法规
    • 人类约定俗称的规则

• Cost function 成本函数

  • 真实情况下许多条可行轨迹
  • Cost由许多条件组成
    • 道路偏离中心线距离
    • 碰撞或靠的太近
    • 速度太快，超速
    • Curature太大，方向盘太急

• 不同场景我们可能有多个不同的cost func

  • 高速场景
  • 停车场
  • 不同车辆

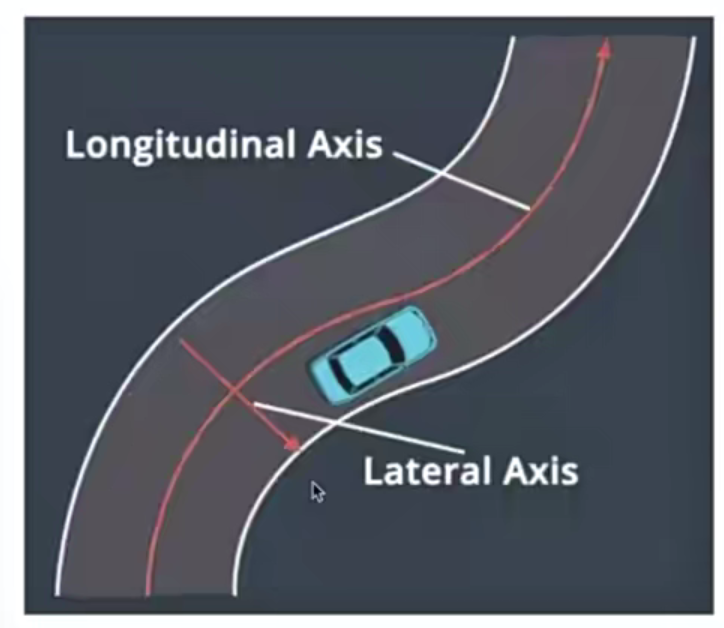
• Frenet坐标系（车道坐标系）

  • 一般我们选用笛卡尔坐标系（世界坐标系)
  • xy坐标无法知道我们车开多远
  • 有没有偏离中心线
  • 也不知道道路在哪里
  • 

• Path vs Speed

  • path Planning
    • 生成可行轨迹路径
    • Cost
      • path 平滑性
      • 安全性
      • 道路中心偏移距离
  • 选择出成本最低的一个Path Planning
  • Speed Planning
    • 每个path上选择一系列速度
    • 生成速度轨迹

• Path Planning

  • 先生成道路网格(GridMap)

  • 每个网格单元中随机采样(撒点)

• 每个网格选一个点

  • 组成多条候选Path ![[Pasted image 20221204201422.png]]

  • Cost Function 对这些轨迹进行评估

    • 找到成本最低的一个
    • 中心线距离$l*a_0$
    • 障碍物距离$d*a_1$
    • 速度变化率$acc*a_2$
    • 曲率$kappa*a_3$

  • $$
    F(X)=La_0+da_1+acca_2+kappaa_3+a_4
    $$

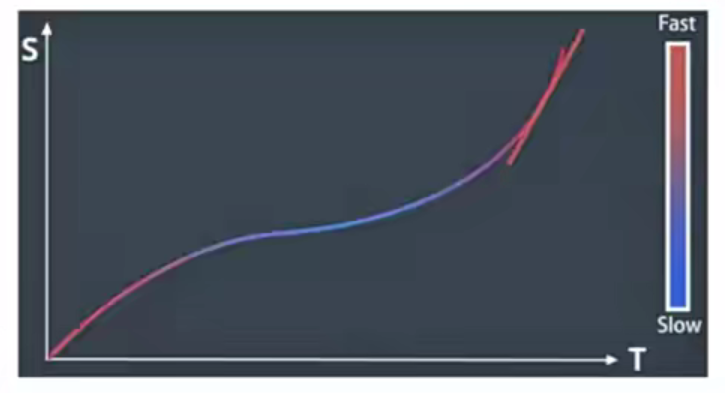
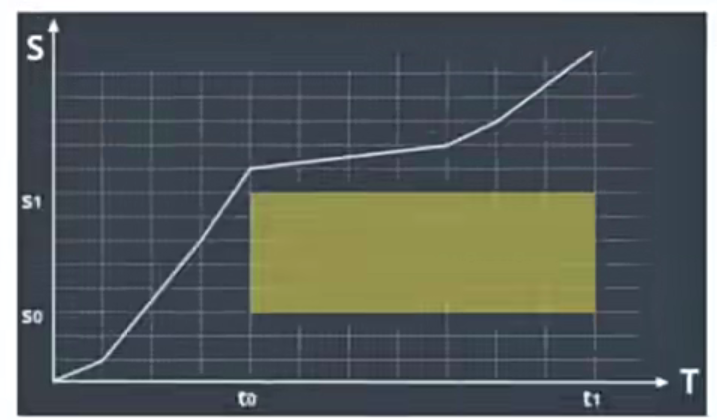
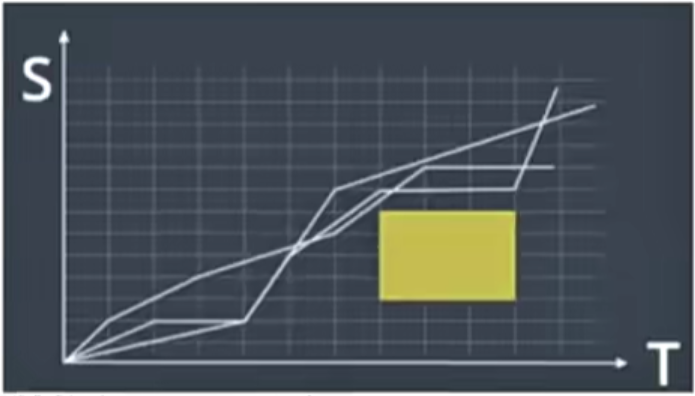
• Speed Planning

  • ST图
    • S表示Path 上的纵向距离
    • T表示运动时间
  • 如何规划ST轨迹
    • 连续空间离散化(grid map)
    • 单元格内速度不变
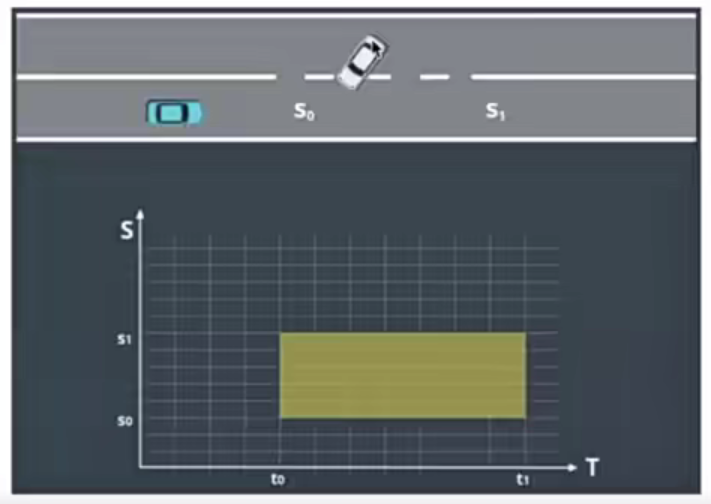
  • 把障碍物投影进来
    • 挡住我们Path轨迹的部分画进ST图中
    • 因此必须要有良好的预测轨迹
    • (下图，to, t1时刻障碍物会在我们的path轨迹中挡住s0, s1部分)
    • 
    • 
  • 如何优化优化 ？
    • 对不平滑的速度线优化
      • QP
    • 我们的这个方法很大程度依赖于连续空间离离散化
    • 网格、单元格方法
      • 但是并不平滑
      • Quadratic Programming二次规划
      • 将平滑的非线性曲线与这些线段进行拟合
      • 现成的工具qpOASES

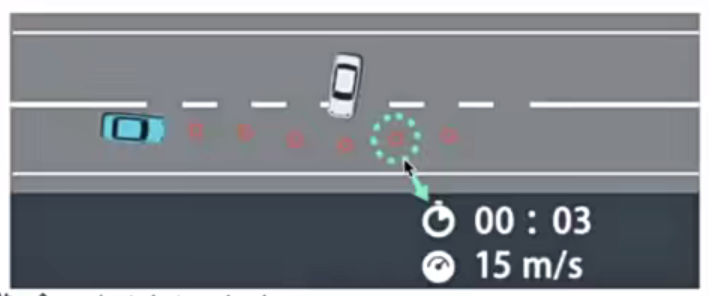
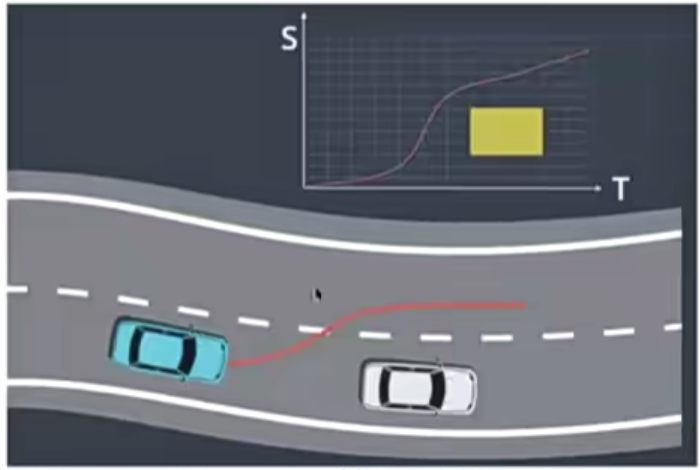
• 轨迹规划

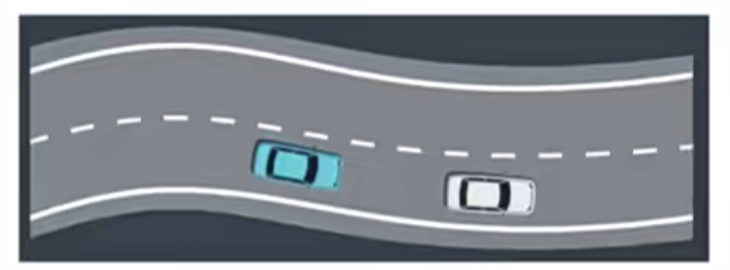
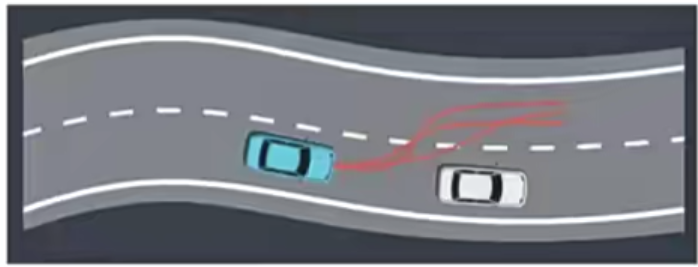
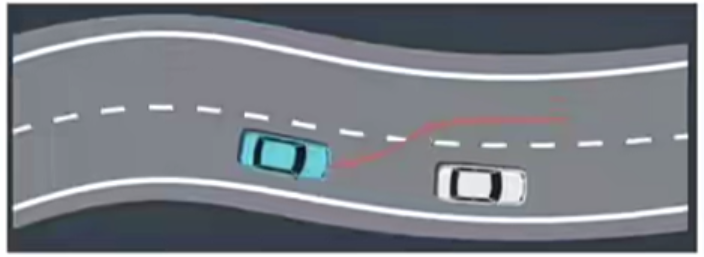
  • 实例：遇到一辆速度很慢的车我们如何超车
  • 生成很多轨迹点（撒点采样）
  • Cost Function 对其进行评估，选择Cost 最小的一条
  • 生成一个ST图来表述速度规划
  • 生成多条速度曲线
  • 使用优化工具对多条速度采样进行最优求解（Cost func, Constraints）
    • 让整个路线和速度曲线变得平滑
    • 

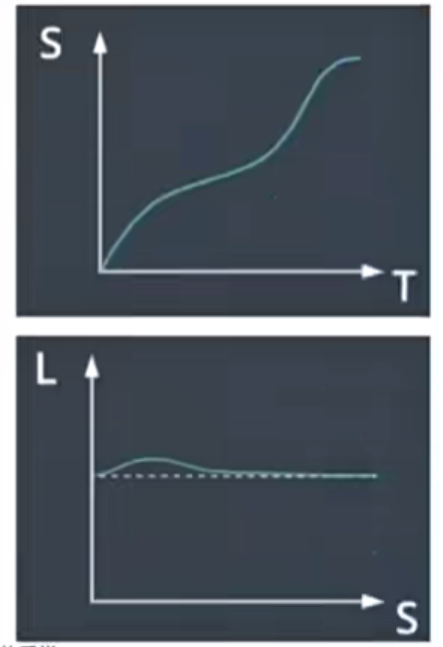
• Lattice Planning (网格规划)

  • SL轨迹和ST轨迹
  • Lattice 将两图合并处理，同时进行Path 和Speed的采样
  • 实例：切车场景
  • 先对整个候选轨迹进行采样
  • 条件检查和碰撞检测
  • 检查失败则返回继续找Cost 次优候选项
  • 成功则输出结果

记录自：七月学院-无人驾驶实战