Divide Areas Algorithm for Optimal Multi-Robot Coverage Path Planning
DARP: Divide Areas Algorithm for Optimal Multi-Robot Coverage Path Planning
* Authors: [[Athanasios Ch. Kapoutsis]], [[Savvas A. Chatzichristofis]], [[Elias B. Kosmatopoulos]]
初读印象
comment:: DARP区域分解,开始使用维诺图进行分配,然后使用评估函数进行评估,更新评估函数。为实现连通,使用了惩罚和奖励的机制。
文章骨架
%%创新点到底是什么?%%
novelty:: 将地形划分为若干个相等的区域,每个区域对应一个特定的机器人,保证完全覆盖,无回溯解,最小覆盖路径,同时不需要任何准备阶段。
%%有什么意义?%%
significance:: 无视初始位置;各机器人工作量相同, 也可根据需求更改进行不同比例的分配。
%%有什么潜力?%%
potential::
%%DARP 实现思路?%%
%%1.初始化区域%%
- 对于每个第 i 个操作机器人,维护一个评估矩阵 Ei。矩阵 Ei 表示 L(空闲栅格的集合) 的细胞与第 i 个机器人的初始位置 χi (t0) 之间的可达性水平(例如距离)。
$$
A_{x, y}=\underset{i \in\left{1, \ldots, n_{r}\right}}{\operatorname{argmin}} E_{i \mid x, y}, \forall(x, y) \in \mathcal{L}
$$
- 然后,每个机器人的区域 Li 可以通过分配矩阵 A 直接计算如下:
$$
L_{i}={(x, y) \in \mathcal{L}: A(x, y)=i}, \forall i \in\left{1, \ldots, n_{r}\right}
$$
每个机器人分配的区域的单元数量
$$
k_{i}=\left|L_{i}\right|, \quad \forall i \in\left{1, \ldots, n_{r}\right}
$$
%%2.等面积方法%%
-
更新分配系数
ki:第i个机器人的实际分配数量
f: 可分配中栅格数除以机器人数量
c: 调整系数
$$
m_{i}=m_{i}+c\left(k_{i}-f\right)
$$ -
控制连通性
其中 Ri 表示第 i 个机器人实际所在的单元的连接集 (χi (t0)),Qi 表示所有其他连接集的并集,这些连接集已分配给第 i 个机器人但它们与 Ri 集没有空间连接。
$$
\mathcal{C}_{i \mid x, y}=\min (|[x, y]-r|)-\min (|[x, y]-q|)
$$
$$
\forall r \in \mathcal{R}{i}, \quad q \in \mathcal{Q}{i}
$$
远离初始位置并且不属于该机器人的区域为一定为正值,相反属于机器人的连通区域一定为负值。从而使得近处被奖励,远处被惩罚。如果全连通则C为全1矩阵。
- 更新评估矩阵
$$
E_{i}=\mathcal{C}{i} \odot\left(m{i} E_{i}\right)
$$
算法思想
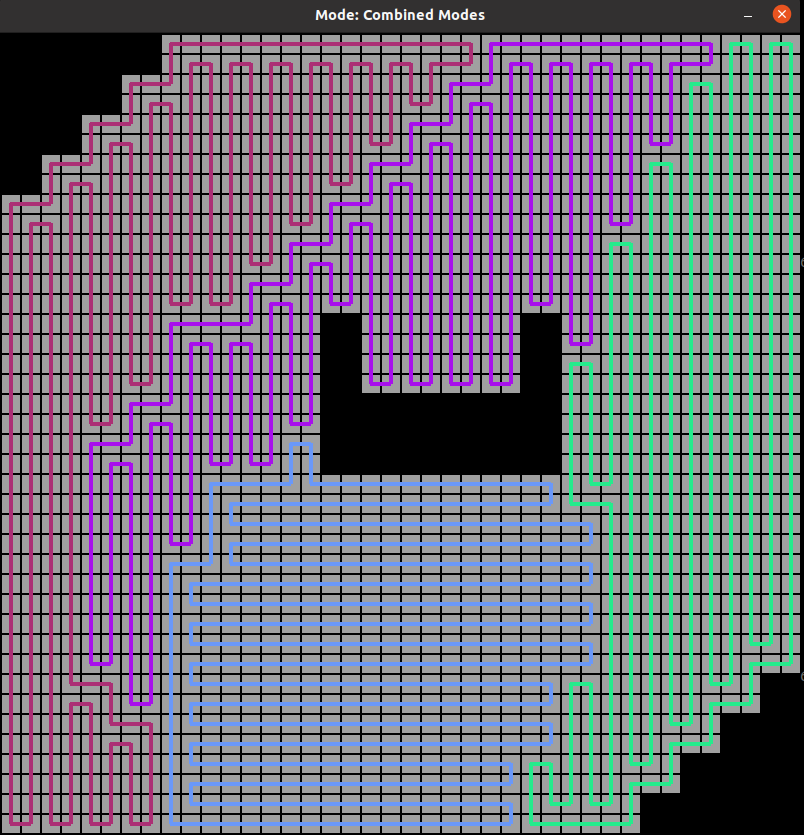
可视化效果
路径规划
使用DARP达到期望的区域划分后,作者使用(生成覆盖树)STC算法为每个机器人生成最优路径,以实现对感兴趣区域的全覆盖。
论文开源代码
[Java] https://github.com/athakapo/DARP
[Python] https://github.com/alice-st/DARP
[c++/ROS]https://github.com/cpswarm/swarm_functions/tree/kinetic-devel/area_division